Radial Basis Function Networks:Empowering Machine Learning Applications

Radial Basis Function (RBF) networks have become a significant tool in the field of artificial intelligence and machine learning for a variety of applications. Radial basis functions are used as activation functions in RBF networks, a subclass of artificial neural networks. They are well suited for a variety of applications, including pattern recognition, function approximation, data clustering, and time-series prediction, because of their distinctive capabilities. This article explores the uses, advantages, and prospective improvements of RBF networks, illuminating their importance in the constantly developing field of machine learning.

Image Source|Google

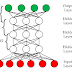
Architecture:

The input layer, the hidden layer, and the output layer are the three basic layers that make up an RBF network's design. In order to process the input data and produce the required output, each layer has a distinct function. Let's investigate the architecture in greater depth.

Input Layer: Raw input data, which can be continuous or discrete variables, is provided to the input layer of an RBF network. A feature or attribute of the input data is represented by each node in the input layer. These nodes' values are just the input values that were sent to the network.

Hidden Layer: The main computation in an RBF network happens at the hidden layer. The input data are transformed into a higher-dimensional feature space using a series of radial basis functions (RBFs). The intricate relationships in the data are modeled by the RBFs, which serve as activation functions for the hidden layer nodes.

An RBF centered on a particular location in the input space is represented by each node in the hidden layer. An activation value is generated by the RBF by calculating the similarity or separation between the input data and its center. The Gaussian function, which measures the distance between the input and the center using the Euclidean distance metric, is the RBF that is most frequently used.

Each hidden node's activation value indicates how similar the input and the related RBF center are to one another. These activation values are given weights by the hidden layer nodes, which highlights the contribution of each RBF to the approximate output. The output layer receives the weighted activations after that for processing.

Output Layer: Based on the information that has been processed from the hidden layer, the output layer of an RBF network generates the final output or prediction. The output layer's node count is determined by the particular task at hand. In regression issues, the continuous projected value is typically provided by a single output node. Each output node in classification issues corresponds to a distinct class, and the node with the highest activation is regarded as the predicted class.

Each hidden node's contribution to the output is determined by the weights between the hidden layer and the output layer. To reduce the error between the predicted output and the desired output, these weights are modified throughout the network's training phase using methods like gradient descent or least squares estimation.

Overall, the architecture of an RBF network combines the flexibility to handle different types of input and output data with the capacity to capture nonlinear relationships through the RBFs of the hidden layer. RBF networks can perform well in tasks including pattern recognition, function approximation, time-series prediction, and data clustering because of this architecture.

Applications of Radial Basis Function Networks:

Pattern Recognition: RBF networks are excellent at applications requiring pattern recognition, such as voice and image recognition. They can effectively classify patterns because they can simulate intricate nonlinear interactions. RBF networks are capable of capturing complex patterns and producing precise predictions because they can map input patterns to a higher-dimensional feature space.

Function Approximation: Complex function approximation is a skill of RBF networks. They are highly precise in their ability to learn and express nonlinear relationships between inputs and outputs. RBF networks can mimic stock prices, currency exchange rates, and other intricate financial systems, making use of this skill particularly helpful in industries like finance.

Time-Series Prediction: Time-series data can be forecasted well using RBF networks. They are able to forecast future values with astonishing precision because they can capture temporal relationships and nonlinear dynamics. Weather forecasting, stock market research, and energy load forecasting are a few areas where time-series prediction is useful.

Data Clustering: Unsupervised learning tasks like data clustering are capable of being completed by RBF networks. RBF networks may allocate data points to suitable clusters based on proximity by putting radial basis functions in the center of clusters. Detecting anomalies, segmenting images, and segmenting customers all make extensive use of this clustering feature.

Benefits of Radial Basis Function Networks:

Nonlinear Representation: RBF networks have the ability to accurately describe and express nonlinear interactions in the data. RBF networks, in contrast to linear models, are capable of capturing subtle and complicated patterns, which makes them appropriate for tasks involving nonlinear data distributions.

Flexible Architecture: RBF networks have an adaptable design that makes it possible for them to handle diverse kinds of data. They can handle inputs and outputs that are both continuous and discontinuous. Additionally, the hidden layer's number of radial basis functions may be altered to fit the difficulty of the issue at hand, allowing for flexibility in a variety of circumstances.

Robustness to Noise: RBF networks are renowned for their ability to withstand noisy data. They may deal with outliers and noisy inputs by giving the appropriate radial basis functions reduced weights, hence minimizing their negative effects on the performance of the whole network.

Interpolation Capabilities: RBF networks perform tasks requiring interpolation very well, enabling them to estimate missing or partial data. When working with irregular or partial information, this trait is useful for RBF networks that can fill in the gaps and provide reliable estimates.

Future Enhancements of Radial Basis Function Networks:

Scalability and Efficiency: The development of scalable and effective training methods for massive RBF networks might be the subject of future study. They may improve their performance and shorten training times by using strategies like parallelization, distributed computing, and adaptive learning.

Automatic Hyperparameter Tuning: Exploring automated solutions may reduce the need for human trial-and-error when choosing the best hyperparameters for RBF networks. To identify the optimum hyperparameter settings for enhanced performance, strategies like grid search, Bayesian optimization, or evolutionary algorithms might be used.

Deep RBF Networks: Promising potential exists in examining RBF network integration in deep learning architectures. Strong hybrid models for diverse purposes may result from combining the advantages of RBF networks' nonlinear approximation skills with deep learning's strengths in feature extraction.

Explainability and Interpretability : In important sectors, improving the interpretability of RBF networks may boost acceptance and confidence. RBF networks may be made more approachable and intelligible to human users by creating methods to describe the decision-making process of RBF networks and provide insights into the significance of certain aspects.

Conclusion:

In the area of machine learning, radial basis function networks have become a flexible and potent tool. Their extensive use across many disciplines is a result of their capacity to perform a variety of tasks and simulate complicated patterns and nonlinear processes. RBF networks are anticipated to continue developing with continuous research and developments, offering even more precise forecasts, increased scalability, and improved interpretability. RBF networks have a bright future and will play a key role in the developing fields of machine learning and artificial intelligence.